
1.
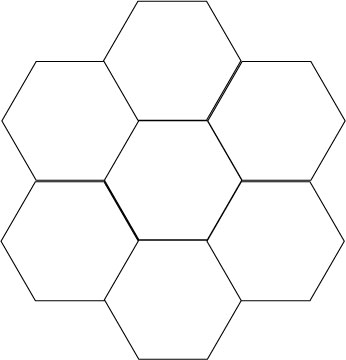
A portion of the plane tiled with hexagons
2.
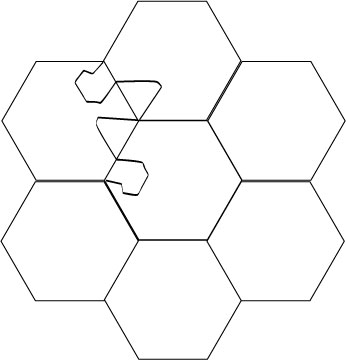
We connect the edges of one of the sides with a broken line.
3.
Rotate for 120 degrees clockwise.
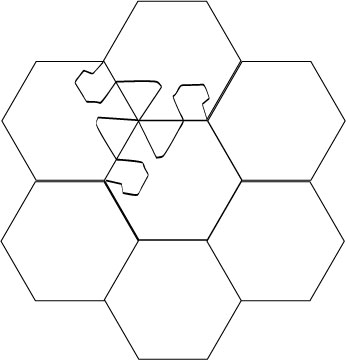

4.
Once again.
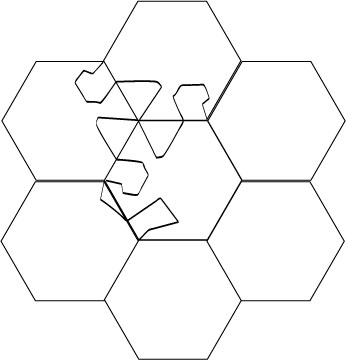
5.
Now connect the edges of another sides with a broken line
4.
Rotate this broken line for 120 degrees clockwise (the canter of the rotation
is clear).

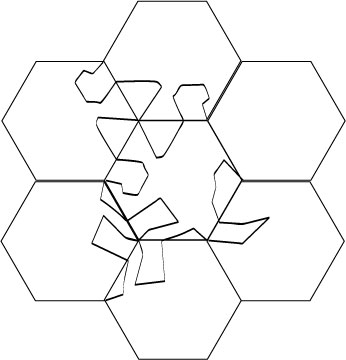
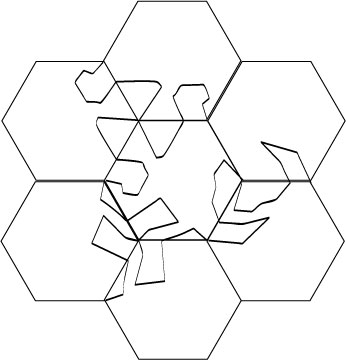
7.
And again.
8.
The last broken line to draw.
9.
Rotate once.

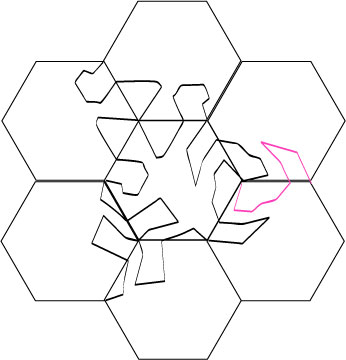
10.
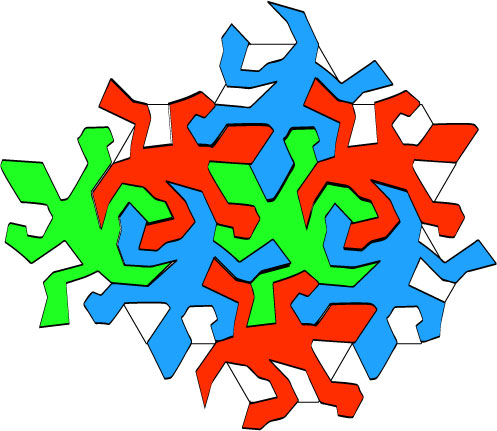
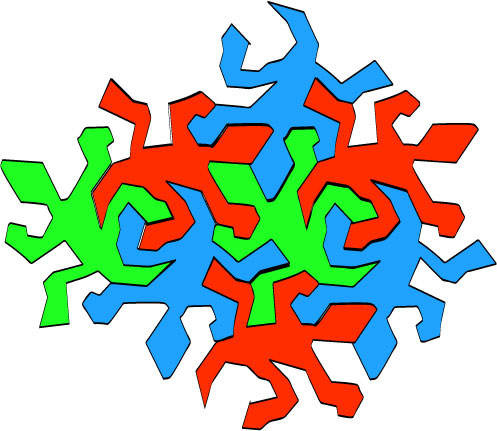
And once more; we see the crocodile.
11.
We now start with translations.
12.
This translations is along 3 times the horizontal vector equal to the
side of the hexagon and pointing to the left.
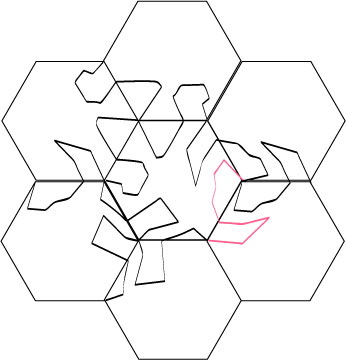

13.
We keep using translations.
14.
Always along vectors 3 times the side of the hexagon.
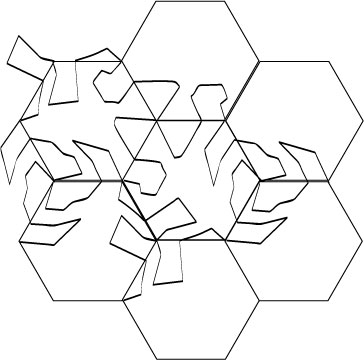
15.
This time the vector is parallel to another side of the hexagon.

16.
All of the translations are along vectors parallel to the sides of the
hexagon.
17.
Which portion has been translated?
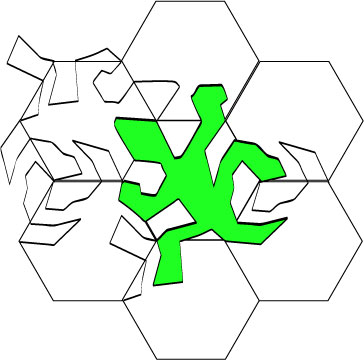
18.
Start with some color.
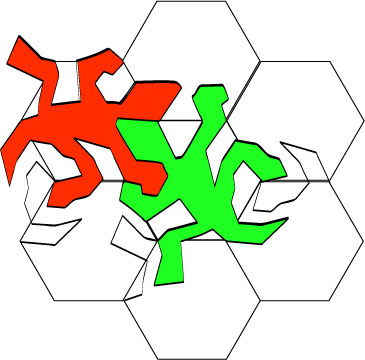
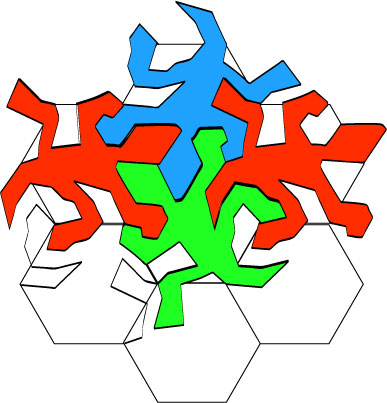
19.
One more croc.
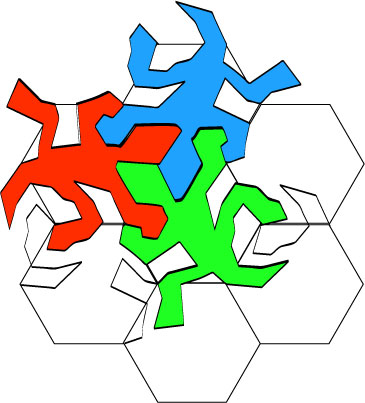
20.
And one more; they fit nicely.
21.
One more.
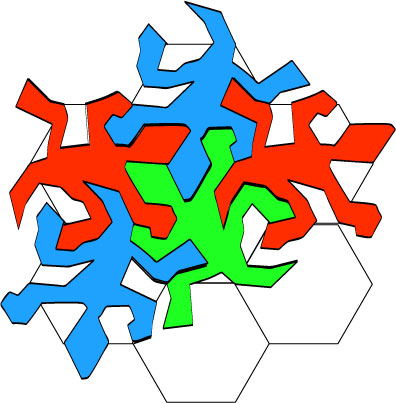


22.
One more.
23.
One more
24.
One more; we can do that ad nauseam.