136.102 Math in Art

Midterm Exam Solutions

February 25 2003

(70 minutes)

1. (a) Use an unmarked ruler and a compass to find the golden cut C of the line segment AB.

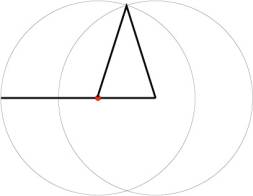
(b) Use an unmarked ruler and a compass to construct a golden triangle with basis equal to the length of the segment CB and the lengths of the other two sides equal to the length of the line segment AC (make a separate picture for (b)).

Solution.

(a)

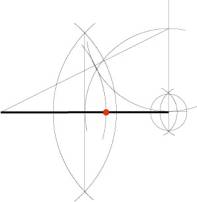
(b)

2. List all of the symmetries of the objects A and B below.

[If you list a rotation as a symmetry then say “a rotation centered at O and for an angle of x many degrees”, where O is a point you should identify in the picture, and x is a specific angle measure you should find.

If you list a reflection as a symmetry then say “a rotation with respect to the line l (or however you call it), where l is a line you should sketch.

You do not have to justify or precisely construct anything in this question]

Solution.

Object A

Symmetries:

1. Identity

2. Reflection with respect to the vertical line passing through the middle of the picture

Object B

Symmetries:

1. Identity

2. Rotation for 120 degrees around the point in the center of Object B.

3. 2. Rotation for 240 degrees around the point in the center of Object B.

As observed by some of you, the arrows at the bottom of the logo are not the same as the arrow at the top (that escaped me). So, the only symmetry is the identity.

3. (a) The object B is obtained form the object A by rotation. Use an unmarked ruler and a compass to construct the center of the rotation.

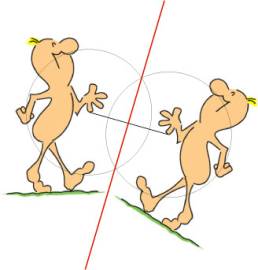
(b) The object D is obtained from the object C by reflection. Use an unmarked ruler and a compass to construct the line of reflection.

Solution (a)

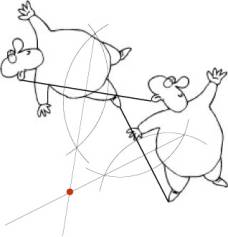
(b)

4. We construct a sequence of rectangles by adding squares over the larger sides of the rectangles (see the picture; assume that the length of the side of the initial square is 1 unit). Draw the next rectangle in this sequence and explain (in not more than 2 sentences) how are the shorter sides of the rectangles in this sequence related to the Fibonacci numbers.

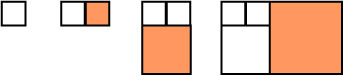
Solution.

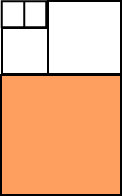
The lengths of the smaller sides of the rectangles are in fact the numbers in the sequence of Fibonacci numbers.

5. The first two stages of a construction of a fractal are given in the picture below. Notice what has been done with each of the line segments of Figure 1 in order to get the shape in Figure 2, and draw the shape obtained after applying this procedure one more step.

Solution.

Figure 1. Figure 2.