136.330 Intro to Algebra
Test 2
(October 30, 2002)
Justify all your answers unless otherwise stated.
1. Suppose 
and K
are subgroups of a group G. Show that
the intersection 
is also a
subgroup of G.
Solution.
0. Since both H and K contain the identity of G, the intersection 
is not empty.
1. Suppose 
. Then 
and 
. Since H is a
subgroup of G, it follows that 
. By symmetry, 
. So, 
.
2. Suppose 
. So 
and 
. Since both H and K are subgroups, we have 
and 
. So 
.
By a theorem, these two properties suffice to claim that 
is also a
subgroup of G.
2. Find the Cayley table of the group of symmetries of
(a) S
(b) H
Solution.
(a) The only symmetries of S are id (the identity) and rot (rotation around the middle point for 180 degrees). The Cayley table is given below.
(b) The symmetries of H are id, rot (rotation around the mid-point for 180 degrees), ref1 (reflection along the middle horizontal line) and ref2 (reflection along the middle vertical line). Here is the Cayley table.
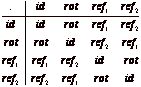
3. (a)
Find all positive integers n
such that 
.
(b) Use congruence to find the remainder if 
is divided by 4.
(Hint:
)
Solution. (a) 
means 
, i.e. 
. So, 
.
(b) Since 
and since
congruence are compatible with multiplication, we have 
, that is 
. But 
and because
congruences are transitive, we have 
. So, (by a theorem) 
and 3 have the
same reminder after dividing by 4. But the reminder after dividing 3 by 4 is
obviously 3; so the same is true for 
.
4. Recall that 
is the structure
consisting of the conjugacy (?) (congruence) classes 
modulo n
and the operation 
defined by 
. Prove that 
is a group.
(Note: we have proven in class that 
is associative
and that [1] is the identity; you may use that result.)
Solution. The note
tells us that it suffices to show that every element in 
has an inverse.
We check: 
(the last
equality is true since 
); hence [3] is the inverse of [2] (and vice versa). Further 
and so [4] is
the inverse of itself. And, of course, [1] is also the inverse of itself.
5. (a) Use the Euclidean Algorithm to find (258, 102).
(b) Prove that if (a,c)=1 and if (b,c)=1 then (ab,c)=1.
Hint. Recall the following theorem: (x,y)=1 iff 
such that 
.
Solution.
(a) 258=(2)102+54
102=(1)54+48
54 =(1)48+6
46 =(8)6+0
So, by the Euclidean Algorithm, (258, 102)=6.
(b) Since 
there are
numbers 
and 
such that 
.
Since
there are
numbers 
and 
such that 
.
Multiply these two equalities to get 
. Expand a bit, get 
. Factor a bit: 
, and finally, observe that the last equality together with
the theorem given in the hint implies that (ab,c)=1.