136.271
Midterm Exam 1
SOLUTIONS
February 27 2003
(60 minutes; justify your answers unless otherwise stated; no calculators)
Note: the marks for the questions add up to 65, for 32.5%
of your mark: the extra 2.5% are bonus.
1. [13]
(a) Finish off the following definition: A sequence 
converges to a
number 
(written 
) if ………
(b) Use the (above) definition of a convergent sequence to show that 
.
Solution.
(a) A sequence 
converges to a
number 
(written 
) if for every 
, there is a number N, such that if n>N then 
.
(b) Take any 
. Want to find N such that if n>N then 
. The last inequality in case of the sequence in this problem
becomes 
, which simplifies to 
, which in turn simplifies to 
, which in turn means 
, or, finally 
. So we want to find a number N, such that if n>N then 
. Choose N to
be any number larger than 
(that is, 
). Then, if n>N
then, 
, and so 
.
2. [22] All of the series in this question are positive. Determine if the given series converges or diverges by using any appropriate test.
(a) 
(b) 
(c)
Solution.
(a) Note that 
and that 
. It follows from the divergence test that the series
diverges.
(b)
We use the limit comparison test with
(which, as we
know, converges).
.
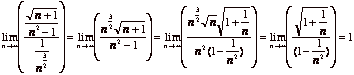Since we got a finite number both series converge/diverge
simultaneously. So, since 
converges, it
follows that 
converges too.
(c)
Consider the function 
, 
. Notice that 
, 
, yields the general term of the series. Also notice that 
is continuous, positive and decreasing (all of these are
obvious). So, we can use the integral test.
=
=
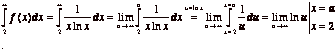
So, the series diverges.
3.[17] Find the radius of convergence and the interval of convergence of the series
(a) 
(b) 
Solution.
(a)We use the ration test: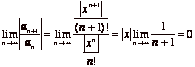 
and since this
is always less than 1 it follows that the series converges for all numbers x.
So, the radius of convergence is infinity and the interval of convergence is 
.
(b) Ratio test: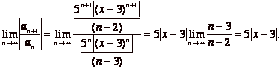 
So, the series
converges when 
. We solve this: 
, where the symbol 
should be read
as “means the same as”. We conclude that the radius of convergence
is 
. To establish the interval of convergence we need to take a
look at the cases when 
and 
.
(i)
. In this case the series becomes 
which converges
by the alternating series test.
(ii)
. Now we have 
which diverges
(by the limit comparison test with 
, say).
So, the interval of convergence is 
.
4. [13] (a) Find the interval of convergence and the sum of (the closed form expression for) the series
(b) Use (a) to compute the sum of the series 
Solution.
(a) For the interval of convergence we use the ration
test again: 
We solve 
, to get 
. It is visible that the series diverges when 
or 
. So, the interval of convergence is 
.
Denote 
. Observe that 
and since,
obviously, 
, it follows that 
and so 
. Since (geometric series) 
, it follows that 
. All t his is true over the common interval of convergence 
. So, summarizing, 
, for x in 
.
(b)
is just the
value of the series in (a) when 
. So, by (a), it is equal to 
.