136.271

Assignment 4: Section 9.8 and Uniform Convergence

(Due April 7 in class)

1.

(a) Use the binomial series to expand . Simplify your answer.

(b) Use part (a) to find the sum of the series . (No marks if other methods are used.)

Solution. (a) According to the Binomial theorem, we have . We simplify a bit

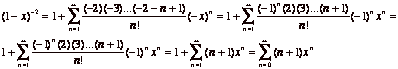
So, .

(b) We observe that is what we get if we put in . So, we get the same value if we substitute in , which is .

2. Given the sequence of functions find the pointwise limit and then show that the sequence converges uniformly to .

(a) over the interval [0,1].

(b) over the interval [1,2].

Solution.

(a) First we find the pointwise limit: . So, for every x in [0,1]. Now we take a look at . We find that . This function is obviously increasing over the interval [0,1], so its maximal value is attained at x=1; so . Obviously, So, the convergence is indeed uniform.

(b) We follow the above procedure: ; we have used the L’Hospital’s rule in the middle equality (we have differentiated the denominator and numerator separately with respect to n. So, and we have the pointwise limit.

For the rest we again consider . This time we have . We find the maximum of this function for x in [1,2] (we differentiate with respect to x): . This is obviously always larger than 0, so that the function increases over [1,2], and so its maximal value is attained at x=2. We compute . Now we find the limit (use L’Hospital’s rule again): and so the convergence is uniform.

3. Given the sequence of functions find the pointwise limit and then show that the sequence does NOT converge uniformly to.

(a) over the interval

(b) over the interval [0,1].

Solution.

(a) Follow the solution of 2(a) to the point when we found that . Our goal now is to show that does not tend to 0 as n tends to infinity. (Note the difference with respect to 2(a): the domain in this question is , not [0,1] as it was in 2(a)). Choose x=n (this value is certainly in . For this choice of x we have that is . This obviously tends to 1 as n tends to infinity (in fact, it is always 1). Consequently, the maximum, which is certainly at least as much as what we get when x=n, could not approach to 0 as n approaches infinity. So, the convergence is NOT uniform.

(b) First the pointwise limit: (we have used L’Hospital again – the differentiation was done with respect to n.) So, . We find that , so that we look for the maximal value of that function over the interval [0,1].We differentiate with respect to x, to get . This is always negative, so that the function is decreasing over [0,1]. Consequently, its maximum is attained at x=0. We compute the value: and the limit of this is certainly not 0 as n tends to infinity. So, the convergence is not uniform, as claimed.