136.271

Assignment 3: Solutions

1. [6 marks] Find the sums of the following series.

(a) , .

(b) .

Solution.

(a) , where the last equality is true because the first two terms are annihilated by differentiation anyway. Continuing, we have .

(b) is clearly the value of the function in (a) when , and so, by (a), it is equal to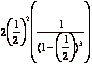

2. [5 marks] Find the Maclaurin series representation of the following functions.

(a)

(b)

Solution.

(a) Since , it follows that .

(b) is an old identity. We know that , so that . Consequently and so .

3. [6 marks] Find the sum of the series.

(a)

(b)

(c)

Solution.

(a)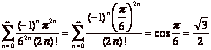

(b) .

(c) Note first that if x=0 then the value of the series is 1. For we do as follows: .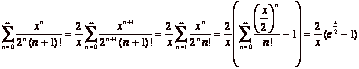

4. [4 marks] Evaluate the following integrals as power series.

(a)

(b)

Solution.

(a) Since for every t, we have that . So

(b) .

5. [4 marks] Show that the Lagrange remainder in the Taylor’s formula for the following functions tends to 0 as n tends to infinity, thus establishing that the functions are equal to their power series representations.

(a)

(b)

Solution.

(a) for some z between c and x. Since here we have that , the n-th derivative of this function is some of and -, so that in all cases . Consequently and by an old result (Section 9.1), the limit of the term on the right-hand side is 0. So the same is true for the left-hand side, so that as wanted.

(b) Start with again. In this case , so that . So, , with z between c and x. There are two possibilities: either (in which case ) or (in which case ). In the former case , while in the latter case . So, , where y is either c or x depending on the two cases just listed above. In both of these two cases is a fixed number independent of n. So, and, using the same old theorem we have used in the part (a) above, we conclude that , so that , so that as wanted.