136.271 Assignment 2 (Sections 9.3, 9.4 and 9.5)

SOLUTIONS

1. [9 marks]

(a) Use the Integral Test to test if the series converges. Do not forget to check that the Integral Test is applicable before you apply it.

(b) Use the Comparison Test to determine if converges.

Solution.

(a) Consider the function for . Note first that gives the general term of the series. The function is obviously positive and continuous. We now show it is decreasing by showing that the first derivative is less than 0 (for ): and this is indeed less than 0 since is always positive, while is negative when . So, the integral test can be used.

, where we have used the substitution to evaluate the integral (the second equality). Since the integral converges, so does the series.

(b) First we notice that (this is true since for ). Since we know (theorem) that diverges, it follows that also diverges. By the comparison test, we have that diverges too.

(c) Compare with the convergent series: 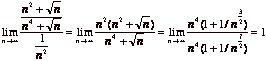, and so the series also converges.

2. [9 marks] Check if the following series is absolutely convergent, conditionally convergent or divergent.

(a)

(b) (the handout contained a printing error in )

(c)

Solution.

(a) We use the Ratio test to check for absolute convergence. 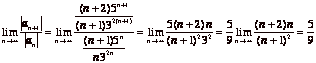and since this is less than 1 we conclude that the series converges absolutely.

(b) Use the Root test: and since this is less than 1 the series converges absolutely.

(c) We check for absolute convergence by applying the limit comparison test on and , knowing that the latter series diverges.

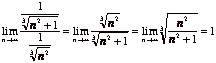, and so, both series converge or diverge simultaneously. Consequently diverges and so the series does not converge absolutely.

To check for (conditional) convergence we use the Alternating series test.

(i) is obviously less than

(ii) .

Consequently, by the Alternating Series Test, the series converges. So, it converges conditionally.

3. [7 marks] Find the center of convergence, the radius of convergence, and the interval of convergence of the following series.

(a)

(b) (the handout contained a printing error in .)

Solution.

(a) . Consequently the series converges absolutely if and it diverges if .

It remains to be seen what happens when , i.e., when or .

Case 1. . In this case the series becomes and this obviously diverges (Divergence Test).

Case 2. . In this case the series becomes and this also diverges (Divergence Test).

So, the interval of convergence is (-1,1), the radius of convergence is 0 and the center of convergence is 0.

(b) 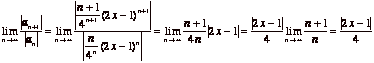. So, the series converges when and it diverges when . Now we solve to describe it more explicitly. , where the symbol reads “is equivalent to” and stands for “means the same as”.

Now we take a look what happens when , i.e., when or .

Case 1. . The series becomes . We simplify a bit: and this diverges by the divergence test.

Case 2. . The series becomes . We simplify a bit: and this also diverges by the divergence test.

Conclusion: the interval of convergence is (-3/2, 5/2), the radius of convergence is 2 and the center of convergence is 1/2.