136.271

Assignment 1 Solutions

1. [6 marks] Show that by using the definition of a convergent sequence and no other properties of sequences.

Solution. Take an arbitrary >0. We want to show that there is an N such that if n>N then

.

We fist examine the last inequality:

, means , means , means . Now the denominator of the fraction in the absolute value is obviously larger that 0 (since n is positive), so the absolute value will not affect it. On the other hand ;so and thus means . We continue: means , means , which finally means . So, to summarize all of this, means the same as . So, we need to find an N, such that if n>N then (i.e. ). That should now be visible: take N to be any number larger than ). Now, if n>N, then (by the preceding sentence) and we got what we wanted.

2. [7 marks] Consider the sequence defined by and .

(a) Compute .

(b) Use mathematical induction to show that the sequence is bounded from above (Hint: show that , say.)

(c) (Optional) Use mathematical induction to show that the sequence increases.

(d) Use (b) and (c) above and refer to a theorem given in class (and in the textbook) to conclude that converges.

(e) Find (Hint: see how we have done that part in the similar examples done in class.)

Solution.

(a) .

(b) We use mathematical induction to show that for every n, .

Step 1. Is ? Yes: .

Step 2. Suppose . We want to show that . We examine our goal again: means , means , means . So, we want to show that if then ! But that is obvious.

(c) Step 1. Is ? Yes, because .

Step 2. Suppose . We want to show now that that would imply . Again we examine our target: means , means , means . So we need to show that (our first assumption) implies . But this could not me more obvious.

(d) Parts (b) and (c) show that the sequence is bounded and increasing. The theorem in class (page 523 in text) implies that it is a convergent sequence.

(e) So we have that exists. Denote it by L. So . Consequently too. So (using the definition of ), we have that . But . So . We solve this to get or . The latter is obviously excluded, since the sequence increases and so the limit must be larger then all of the terms. We conclude that .

3. [6 marks] Use what was covered in section 9.1 to evaluate the following limits.

(a)

(b)

Solution.

(a) .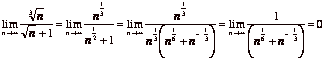

(b) .

4. [6 marks] Find the sum if the series converges; otherwise show it diverges.

(a)

(b)

(c)

Solution.

(a) .

(b) diverges because (and so, it is not equal to 0 – see the divergence test in 9.2).

(c) First find A and B such that : multiply both sides by to get , rearrange to get equate the coefficients in front of the powers of n to get , and solve to get and . So . So, . Lets take a look at the partial sum: where I have put the middle parenthesis just for emphasis. Now cancel the terms that could be cancelled to get that Take the limit of this: . Since (by definition) the sum is in fact , it follows that .