136.271 Assignment 1

Solutions

1. Use only the definition of the limit of a sequence to show that .

Solution. The question is easier than intended. The point is that , so that the problem reduces to showing that . According to the definition we need to show that for every , there is an N such that if n>N then , where is the general member of the sequence and is the claimed limit. However, in this case = and so is in this case , i.e. which is true by assumption. Consequently, whatever N we choose, if n>N we would have because the latter is always true.

Note: In the intended problem it should have been .

2. Consider the sequence defined by , , n=1,2,3,….

(a) Write down the first 5 members of that sequence.

(b) Use induction to show that the sequence is bounded.

(c) Use induction to show that the sequence increases.

(d) Find the limit of that sequence.

Solution.

(a) , , 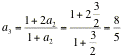=1.6, , .

(b) Showing that, say, for every n. That is obvious for . Assume it is true for some . That is, suppose . We want to show that . Since , the last inequality is . Multiply both sides by the denominator to get , which, after a bit of cancellation becomes , which is obviously true since the right hand number is positive.

(c) Clearly is less than . Assume . We want to show that under the last assumption we have . Recall again that and .

So, the last inequality can be written as (keep in mind: that is what we want to show). After multiplying by that inequality becomes , which, after expanding and canceling reduces to - precisely what we have assumed. So, is indeed true under the assumption that .

(d) It follows from (b) and (c) and from the theorem on monotonic bounded sequences that the sequence converges. Suppose . Then . Now we start from again and apply limit to both sides. We get , which after solving (and throwing away the negative solution) yields (the golden ration that we have encountered in class – recall Mona Lisa).

3. Which of the following sequences converge, which diverge? If a sequence converges find the limit. (You may use the properties and theorems we have stated in class.)

(a)

(b)

(c)

(d)

Solution.

(a) This is the sequence of alternating 0-s and 2-s. It obviously diverges. It was not necessary in the following in the assignment: can you justify that claim using the definition of limit?

(b) (the first step is justified by the fact that all limits exist.

(c) Set . Then, obviously, n=1,2,3…. According to our theory, it suffices to find , and would exist and be the same. We have 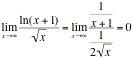(we have used L’Hopital’s rule in the first step.

(d) .

4. Which of the following series converge, which diverge? If a series converges, find its sum, and if a series diverges give reasons.

(a)

(b)

(c)

(d)

Solutions.

(a)

(b) and this diverges according to what we know about geometric series.

(c) First find two number A and B such that ; that reduces to solving a linear system with two unknowns; we get . So, we need . We simplify a bit: and we tale a look at partial sums associated to the last series: . All the inner terms simply cancel out, with the only survivors being the first and the last term. So . It is then easy to see that , so that too. Consequently .

(d) Since (class or text), it follows by the divergence test that diverges (to infinity).