Volumes by Slicing

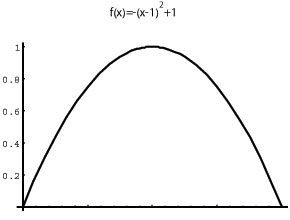
Start with f(x)=-(x-1)^2+1 and rotate around the x-axis the region R bounded by that function and the x-axis.

We get a solid of revolution. You can play a bit with that solid by clicking HERE. (The graphics is interactive: drag or shift-drag on the image. Once you are done, please press the back button on your browser to return here). When we use the method of slicing we initially approximate the solid with another solid made of disks (or slices). You can see the latter HERE. The volume of this solid can be computed using elementary geometry formulas. That volume is an approximation of the volume of the original solid. I have cut both solids at half, emptied their interior and put one of the surface into the other to SEE (please click) how similar they are.

Volumes by Shells

We start with the same region R as above, but now we rotate around the y-axis. We get another solid or revolution (please CLICK to see the surface (minus the base) of that solid - keep in mind that it is the solid we are after). This time it is convenient to use cylindrical shells to get an approximation of that solid. The surface of the solid that we use is now made of cylindrical shells and can be VIEWED AND MOVED. It gives us an approximation of the original solid and its volume can be readily computed using elementary geometry. We can then find the volume of the original solid by taking the limit of the volumes of the solids made of shells as the number of shells tends to infinity. That leads us to the integral yielding a formula for the volume of the original solid.

© S.Kalajdzievski