Midterm 136.152 Solutions

(Monday, June 3, 10:45-11:45)

No calculators; closed book; show your work.

1. We invest 3000 at the annual interest of 5%.

(a) What will the balance be after 7 years if the interest is compounded monthly. You do not have to simplify your answer.

and in this example we have .

(b) Suppose the interest is compounded continuously. How many years it will take to get a balance of 10000. Leave your answer in logarithmic form.

The formula applies. We want t such that . Solving :

and so .

2. The cost of producing x many gadgets is . We sell the gadgets at the price of 15$ per one.

(a) Express the profit function in terms of the number of produced/sold gadgets. Sketch the graph of the function .

The revenue is , and so the profit is . The graph is shown below.

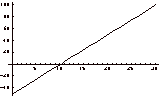
(b) Find the break-even price.

Solve , i.e. , to get .

(c) What is the average cost per one gadget between the levels of production of and items?

. [Note: full mark if the formula for the average cost of producing x items was used in a sensible way.]

3.

(a) The population of Lemmingland was 1000 in 1950 and grew exponentially between the years of 1950 and 1970. After 10 years (in 1960) it was 5000.How many lemmings were there after 20 years (in 1970)? (To answer this question you will first need to find the growth constant). Leave your answer without simplifying it.

Since after 10 years there were 5000 lemmings we have . We solve for k to get , then and so .

We can now find the number of lemmings after 20 years using the formula ; get

.

(b) Between the years of 1970 and 1980 the population fluctuated, and since 1980 it decayed exponentially according to the formula , where is the number of lemmings and is the number of years since 1980. How many years till the population drops back to 1000 lemmings. Leave your answer in logarithmic form.

Solve for t; get , then and so .

4. Evaluate the following limits.

(a)

(b)

(c)

As x approaches 2 from right, x-2 approaches 0 through positive numbers. The numerator tends to –4 as x tends to 2. Consequently the fraction in the limit tends to . So = and it does not exist.

5. Consider the function .

(a) Evaluate .

(b) Find such that is continuous everywhere.

Since does not exist, no k will make this function continuous.

[You get the full mark for doing the following (even though it is incomplete and contains an error): The function f is continuous if . was found to be 2 in part (a). On the other hand, . So, it has to be that k+2=2 which yields k=0 (forgetting the part regarding f(1)).]

6. Use the definition of derivative to find if .

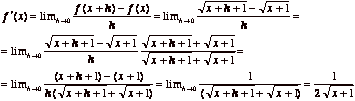
7. Find the equation of the tangent line to the curve at the point when . Justify your answer using the methods covered in the course so far

The equation is where is a point on the line, and m is the slope of the line. We find (given), , and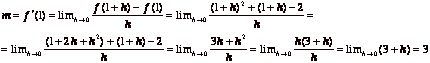

So, the equation of the tangent line is .