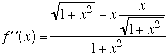Values
[16] 1. Evaluate the following limit or show it does not exist. If the limit does not exist, then determine if it is 
or neither.
(a) 
(b) 
(c) 
(d) 
.
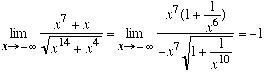
[10] 2. (a) State the definition of the derivative 
of a function f(x) when
x = a.
(b) Use only the definition of derivative to compute 
if
.
[10] 3. The curve 
is defined by the equation
, and the
curve 
is the graph of the function 
. Show that the tangent line to the curve at the point (1, 0) is perpendicular to the
tangent line to at (2, 3).
[Since the minus (in red above) was missing due to a printing error, you were only expected
to find the slopes of the two lines as in the solutions below.]
, so 
; put x=1 and y=0 and solve for y’ to get 
. This is the slope of the tangent to the curve .
For the other curve we find 
and further 
(the slope of
the tangent to that curve at the given point).
[9] 4. Prove the product rule: if f(x) and g(x) are differentiable functions, then
.
[See class notes or textbook]
[15] 5. Use various rules of differentiation to evaluate the following
(Do not simplify):
(a) 
if 
(b) 
if 
if 
