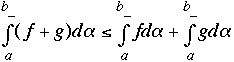
Assignment #6 (2)
Comment and Solution for Q.7.11 (b):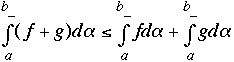
The problem in this question is to show where exactly the strict inequality could occur.
Lets see: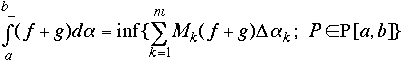 
,
where 
is the supremum of 
over 
.
This supremum could be strictly smaller than 
over the same subinterval. An example where this happens is when f is 1 over
rationals and -1 over irrationals, with g being the negative of f. There is
one more sticky point and we continue further.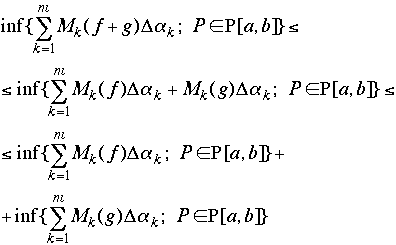 
It
is easy to show that the last inequality is true (hence to get a solution of
the problem) . What may not be so easy is to see if that inequality could also
be strict ! Notice that on the right hand side of the last inequality we could
take different partitions, one for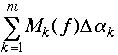 
,
and the other for 
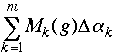while
on the left hand side of the last inequality, both these sums use the same partition
P.