First we show that is continuous at 0 and that it is 0 there. We have: . Instead of doing that limit it will be useful to take a look at where k is any number (for our purposes, suffices to look at numbers k„1). Use the substitution to change it to , which is equal to 0 (use L'Hospital). In particular is also 0 and so exists and is 0.

It is very easy to show (formally, by induction) that if x is not 0, than any is of the form 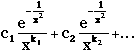for some constants . With that and using the inductive assumption that exists at 0 and is equal to 0 there, we have 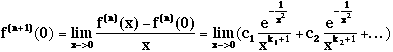, which, by what we have shown above, is equal to 0.

increases if >0. Since , the last inequality is equivalent to . Apply the MVT over [0,x], x in (0,1), to the function : there is a c in (0,x) such that . Since is increasing, we have , and so (what we wanted).

5.21. First note that all are continuous (since exists).

Since f(a) and f(b) are both 0 and since f is non-negative, these are local minima and so . Also, f(a)=0=f(b) in combination with Rolle's theorem give us some d between a and be with . Now apply Rolle again to and to To get two points ( and ) for which . Now apply Rolle to for the last time to get a point c for which .