Since converges, the sequence of partial sums, also converges, and is thus bounded by some number M. We now look at the partial sum of the functional series (I prefer "x" to "s" (used in the statement of the question)). It straughtforward to see (just cancel some terms) that

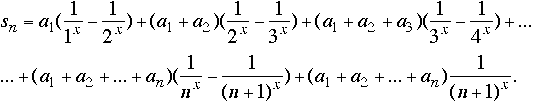
Using , we can write the last formula as follows:

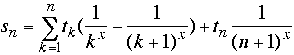. So, .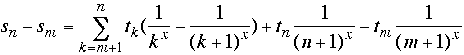

We now look at the absolute value (about to use the Cauchy criterion for unifrom convergence).

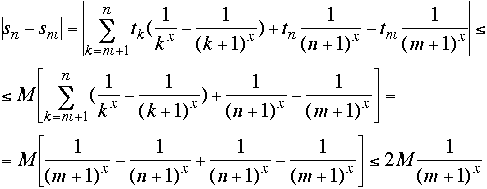
The proof will be completed once we show that the sequence of functionsconverges uniformly for x (strictly) larger than 0. That, by the Cauchy criterion) would make the series uniformly convergent for x>0, and (since it converges when x=0), uniformly converget for non-negative x (what we wanted to show).

So now, we show that converges uniformly for x>0. It is obvious that the pointwise limit of that sequence is 0. So, we need to show that the supremum of over x>0 converges to 0. It is obvious that for each n, the function , x>0, decreases. So, the supremum of that function is and so we are trying to establish that . (Now that is Calculus 3 - 2nd year ). Assume n>1 and look at the function . Put and apply double limit as and (the latter being equivalent to ). The we get , so that indeed .