136.271
Midterm Exam 2
November 17 2000
(50 minutes; justify your answers unless otherwise stated; no calculators)
1.[5] Find the radius of
convergence and the interval of convergence of the series
Use the ration test:
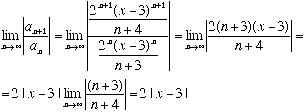
The series converges if 
<1,
which means that 
, which in turn
gives 
and so 
.
We see that the radius of convergence is 1/2. We now look at the edges of
the interval of convergence:
(a) 
. The series in this case
is (after a bit of cancellation) 
which
converges (alternating series test).
(b) 
. In this case the series
is 
. It diverges
So, the interval of convergence is [2.5,3.5).
2.[5] Find a power series representation for the function 
.
First we find a power series representation for 
.
We have 
.
The series converges for 
, i.e.,
for 
. So, in that interval we
have 
and so 
.
[Alternatively, since 
we
have 
and so 
.]
3.[5] Find the sum of the series 
.
.
4.[5] Find the Maclaurin series representation for the function 
.
Show that 
is equal to its Maclaurin
series representation.
So, 
(with 
)
and so 
is the Maclaurin series
representation for the function 
.
To show that 
we need to show
that the remainder 
tends to
0 as 
(with X between 0 and
x). We have 
and, as we have
seen it many times, the last limit is 0.
3.[5] Use binomial series to expand 
as a power series and then find the sum 
.
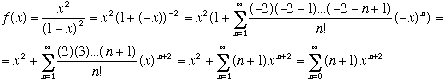
To get the sum 
notice that this
series is what we get above for 
.
So,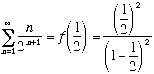 
.