?)136.271
Midterm Exam 1
October 16 2000
(50 minutes; justify your answers unless otherwise stated; no calculators)
1.[5] (a) State the definition
of a convergent sequence. (What does it mean to say that
?)
means that for every 
there exists a number N such that if n>N then 
.
(b) Use only the definition in (a) to prove that 
,
where 
.
Let be any positive number. Looking
for N such that if n>N then 
.
Since ,
means 
which in turn is equivalent
to (means the same as) 
which (since
is positive) is equivalent to
, which is equivalent to 
.
Now take any N larger than 
. Then
if 
, then 
would also be larger than , which,
as we have seen above, would make .
2.[5] Find the sum of the series 
.
Do not simplify your answer.
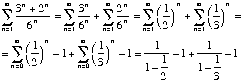
3.[10] Determine if the following series converges by using the indicated test of convergence.
[5] (a) 
, use the integral
test (check if it is applicable first).
Consider the function 
for 
.
In order to apply the integral test we need to check that 
is positive and continuous (for )
(both are obvious) and that (a) is
decreasing.
(a) Suffices to show that 
. But
which is obviously ¾0 for .
So the series converges if and only if the integral 
converges. Now we find
[In the step (*) we have used integration by parts (with 
),
while in (**) we notice that both limits are 0 (the first one dealt with in
part (b) above).
[3] (b) 
. use the limit-comparison
test.
Compare with 
(which we know is convergent):
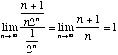. By the limit-comparison test,
converges too.
[2] (c) 
use the root
test.
We look at 
: 
.
So, by the root test (since 
), the
series converges.
4.[5] Check if the series 
is absolutely convergent, conditionally convergent or divergent.
First we check if the series converges absolutely, i.e., if the series 
coverges. We use the limit comparison test and compare with 
:
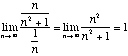so the two seriers converge or diverge
simultaneously. Since , so does .
So, does NOT converge absolutely.
Now we check if it converges (conditionally). Since
is an altternating series, we can check if the alternating series test is applicable.
For that we need to show
(a) 
and that (b) 
is a decreasing sequence.
To check (a) suffices early calculus 1. So we look at (b): we need to show
that 
. The last inequality is equivalent
to (after multiplying) 
. We expand
and then multiply to get 
,
and, after cancelation, 
which is
obviously true for 
.