.Mini quiz #6 (mini exam) for 1.6%
(Dec.3.2000)
1. (a) State the definition of .
For every 
>0
there should be N such that for every n>N, we have 
.
(b) If 
for all n, use the definition to show that 
.
Take
any number >0. Take N to be ANY number. Then for any n>N we have 
and that is surely < than .
2. Which of the following series do NOT converge
(no justification needed): (a)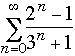 
(b)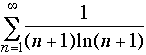 
(c) 
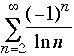(d)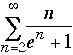 
Only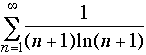
diverges (use the integral test to confirm that). Use various tests to see that
the other 3 series converge.
3. Suppose 
converges and let 
be the n-th partial sum of that series. Find 
.
Since
converges, it follows that 
exists. Since
exists, so does 
and these two are equal. So 
.
4. Circle the values of x for which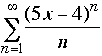 
converges. (a) x=0 (b) x=1 (c) x=3/5
The series converges only for x=3/5. In fact, the interval of converges for the series is [3/5, 1).
5. Find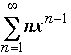 
for -1<x<1. Justify your answer.
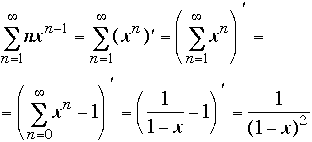
6. Find the
Maclaurin series representation for 
.
We know that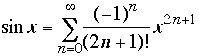 
.
So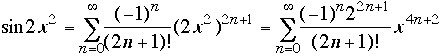 
.
7. Which of the following sequences of functions converge uniformly to 0 over the interval [0,1] ?
(a) 
(b) 
(c) 
The first two converge uniformly to 0 (the maximal
distance between 
and 0 in both cases is 
which obviously converges to 0 as n tends to infinity).
does not even converge pointwise to 0 over [0,1] (it converges to 1 for x=1).
8. Find the Fourier representation of the
function 
,
,
for all x.
It is just that:
! That is, 
,
while the other coefficients 
are all 0.