136.271

Midterm Exam 1

October 17, 2001

(50 minutes; justify your answers unless otherwise stated; no calculators)

1. (a) State the definition of a convergent sequence. (What does it mean to say that ?)

For every there exists a number N such that if then .

(b) Use only the definition in (a) to prove that .

Let . We want to find N such that if then . The last inequality can be changed (without affecting its meaning) as follows: means , means (since the term in the absolute value is positive) , means , means . This is what we want to happen for certain numbers n (those larger than some N). Choose N to be any number larger than . Now we check if the conclusion in the definition of limit is satisfied. Suppose . Then (since ) we have that . But, as we saw above, the last inequality means the same as and so the desired conclusion holds.

 
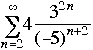  1. Find the sum of the series . Do not simplify your answer.

    2.

     

     

     

     

     

     

     

     

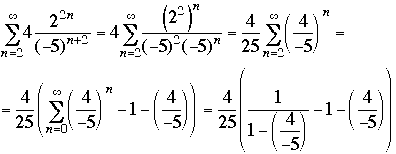
    3. Show that the series converges. Justify your answer.

    The following is a solution in which we only use the Simple Comparison Test; there are alternative simple solutions.

    First note that all the terms are positive, so we can use any of the tests for convergence of positive series.

    Since for , it follows that . On the other hand, it is obvious that . Now the series converges (since converges). By the simple comparison test, the original series also converges.

     

     

  2. (a)
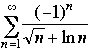. Does it converge absolutely, does it converge conditionally, or does it diverge?

First we check for absolute convergence, that is, checking if 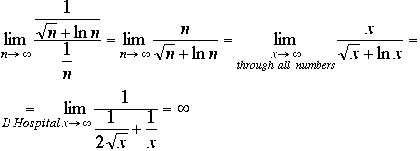converges. We use the limit comparison test and compare with . Compute: Since diverges, it follows from the limit comparison test that also diverges.

So, the original series does not converge absolutely.

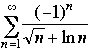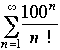
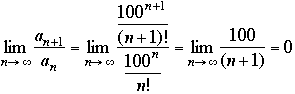We check for conditional convergence — that is, we check if converges. This is obviously an alternating series. So, we may try the Alternating Series Test. For we check if for all n and if . Both are obvious. So, the series converges, and so it is conditionally convergent.

 
    1. . Does it converge? Use the ratio test.

      2. . By the Ratio Test, the series converges.

       

. Does it converge? Use the integral test (first check it can be

used!).

The series is positive. We look at the function for . It is positive, continuous and decreasing (all are obvious). We have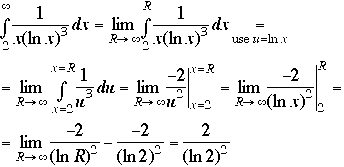

So we got a finite number. By the Integral Test, the original series converges.