Value

[6] 1. Give an example of a function which is continuous everywhere but has no derivative at the point when . Provide a formula as well as the graph of your function.

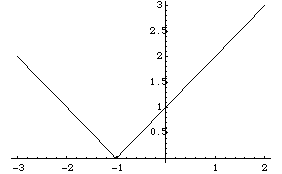
One example is . The graph of that function is given below:

[7] 2. (a) Find the second derivative of the function .

(b) Find if . Do not simplify.

(a) ;

(b) ; so

[7] 3. A particle is moving along the x-axis and the (signed) distance from the origin is given by the formula , where t is time measured in seconds.

(a) What is the velocity of the particle at the moment when the time t is 2 seconds ? (Do not simplify your answer)

(b) Is the particle moving to the right (toward the larger positive distances) or to the left at that moment ? Justify your answer in one sentence.

(a) the velocity is . At the moment when t is 2 it is .

(b) Since the velocity at that moment is and is positive, the particle moves to the right at that moment.

[5] 4. Find if .

Using the Chain Rule, we get

Alternatively, one may use the Extended Power Rule.