Midterm Solutions
1. Evaluate the limit (or explain why it does not exist)
(a)
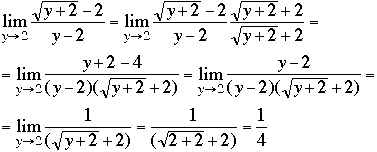
(b) 
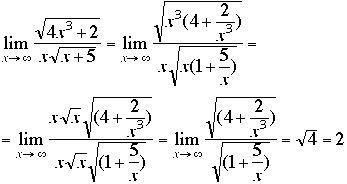
2. Is the function 
differentiable at 
? Justify your answer using only the definition of derivative.
The right hand side derivative at x=0 is 
. We find 
(we have used that here |h|=h). For the left hand side derivative we have 
(we have used that h<0 so that |h|=-h). Since these two are not equal the function is not differentiable at x=0.
3. Do the curves 
and 
intersect perpendicularly at the point 
? Justify your answer!
It is easy to check that 
and 
satisfy both equations, so that is a point where the curves intersect.
For the first curve we have 
and at the point when we have 
. This is the slope of the tangent line to the curve at the point when .
For the second curve we have 
and when we have 
. This is the slope of the tangent line to this curve at the point when .
Since the above two slopes are negative reciprocals of each other the tangent lines are perpendicular and so the curves are also perpendicular.
4. Find the derivatives of the following functions. Show your work and do not simplify your answer.
(a) 
. We have:
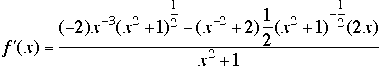
(b) .
. We have:
5.If 
, find 
at the point when and 
.
Differentiate implicitly to get 
. Now substitute and to find that 
, so 
, so 
.
6. [bonus question] Find functions 
and 
such that both are discontinuous at , but 
is continuous at .
Define 
and 
. Then both are discontinuous at . However their product is 0 everywhere, and so it is certainly continuous everywhere.