1. Can Cramer’s rule be used to solve the system 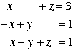? If yes, find x only.

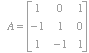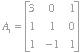Solution. The coefficient matrix is . We compute . So Cramer’s rule can be applied. Set . Then .

2. Suppose 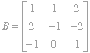. The adjoint matrix of is 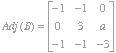. Find .

Solution. The number is in the position (2,3) in the adjoint matrix, so it is the (3,2) cofactor of . We compute .

3.  Is the set a set of linearly independent vectors? Does span the space ? Justify your answers.

Solution. Put these vectors in columns to get the matrix 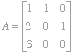. The determinant of that matrix is 3 and so is invertible. It follows from our theory that the set is both linearly independent and it spans .

4. Is the set of all vectors a subspace of ? Justify your answer.

Solution. The set is the solution space of a system of homogeneous equations (just one equation). So, by our theory, it must be a subspace of .