B07. 136.130: Test #3 Solutions
1. Suppose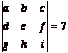 
and 
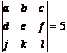. Compute 
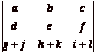and 
.
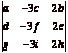Solution. By a theorem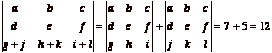 
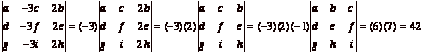
2. Suppose A and B
and both 4 by 4 matrices and suppose 
and 
. Find 
and 
.
Solution. 
3. (a)
Use cofactors to compute the determinant of the matrix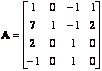 
. (Hint: Use a row or a column which makes the computation
easy).
(b)
State Cramer’s rule for systems with three unknowns and three equations and
use it to solve only for x in the following system
[NO marks will be given if other methods are used.]
Solution. (a)
Expand along the second column: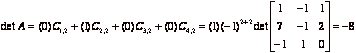 
.
(b) Cramer’s Rule: If
the unknowns are x, y and z,
if the coefficient matrix of the system is A, if the free coefficients are 
, 
and
, and if A is
invertible, then 
, 
and 
where we get 
by putting the
free coefficients in the column number j.
Using this we have: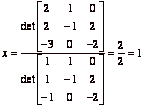 
.