[10] 1. Consider the following system of equations:
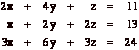
(a) Write down the augmented matrix for this system.
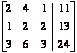
(b) Find the reduced row-echelon form of this matrix.
Row reduce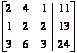 
to get 
.
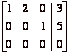(c) Solve the system; present your answer in parametric form.
The system associated to the last augmented matrix above is
Choose y=t to get the solution in the parametric form: x=-2t+3, y=t, z=5.
[10] 2. (a) Let 
, 
, 
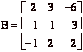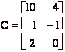
Find, if possible, 
, 
, 
, 
and 
.
1. 
.
2. 
.
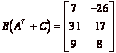3. 
is not doable.
4. 
is not doable.
5. Note that 
is the transpose
of 
. So,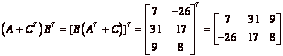 
.
(b) Let A
be a 
matrix,
C a 
matrix,
and suppose that 
.
What are the sizes of the matrices M and B?
Since A is 2x3 and C is 4x5, it follows that B is 3x4 and that M is 2x5.
[10] 3. Let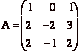 
.
(a) Find 
.
Use row reduction or AdjA to get
that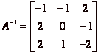 
.
(b) Use your
answer in (a) to solve the system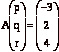 
.
(Full marks will not be awarded for solutions that do not use (a)).
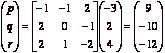
[10] 4. (a) Which of the following matrices are elementary matrices:
, 
. 
,
, 
, 
.
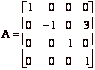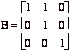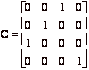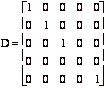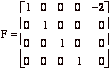B, C and E are elementary; the other matrices are not elementary.
(b) Let 
. Write C
as a product of elementary matrices.
Row reduce: 
. The first matrix is C, the last is the identity. Call the
second matrix 
. The third matrix is already elementary; call it 
. Note that we can get 
from 
by multiplying
the 1st row by –1. So, 
, where we get 
by multiplying
the first row of I by –1; so 
. Further, we can get C from 
by multiplying
the 1st row by (-4) and adding that to the second row. So, 
, where we get 
by multiplying
the 1st row of I by (-4) and adding that to the second row; so 
. Summarizing: 
Note: this is NOT the only correct answer.
.
[10] 5. (a) Compute 
by using
row operations to put the matrix in upper-
triangular form. (Full marks will not be awarded for any other method.)
Start with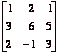 
and row reduce a
bit: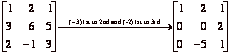 
. Note that the two row operations we have applied so far do
not affect the determinant. One more step:
. This row operation affect the determinant by a factor of
–1. So the determinant we want is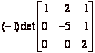 
. But since this matrix is triangular, we have 
.
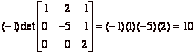(b) Given
that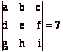 
, find 
.
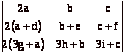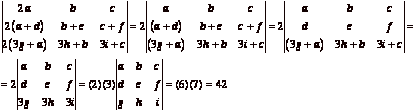
(c) A, B, C are 
matrices
with determinants 
, 
and
. Find 
.
.
[10] 6. (a) Use
Cramer’s rule to find the value of
in the
system:
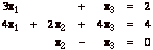
The coefficient
matrix is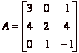 
and 
The matrix 
we need to solve
for 
is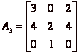 
, and it has the determinant of –4. So, 
.
(b) Suppose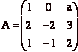 
and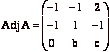 
.
Find
the values of a, b, and c, and use Adj A to find
We read from AdjA that the
cofactor 
is 1. On the
other hand, we see from the matrix A that 
. So, 
, from where we find 
.
Notice that 
. We then compute 
from the matrix
A to get that b=1.
Finally, notice that 
and we find from
A that c=-2.
Now that we know a we compute 
. Since 
, we have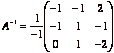 
.