Name:_____________________ Student Number: _______

[8] 1. Find an equation of the line passing through P(1,2,3) and parallel to the line given in parametric form by .

The vector (2,-1,0) is parallel to the given line (we read it from the equation: just the coefficients in front of the parameter t. It is then parallel to the line we want. So, the equation of the requested line is (in point parallel form): .

[8] 2. Find the point normal equation of any plane that is parallel (not overlapping) with the plane .

Since the planes are parallel, any vector orthogonal to the given plane is also orthogonal to the one we want. We see from the equation that is orthogonal to the given plane. So, it is orthogonal to the requested plane. We need one point not in the given plane; take for example O(0,0,0); it is not a point in the given plane since its coordinates do not satisfy the equation. We can now spell the point normal equation of the requested plane:

[8] 3. Use elementary operations to solve the following system.

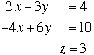
What is exactly the solution set?

After adding twice the first equation to the second we get the following system:

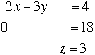
The solution set has not changed. We now observe that the second equation has no solution; consequently the last system has no solution, and so the original system has no solution too. The solution set is the empty set.